

If the value of “x” lies within that range , then we should use the definition
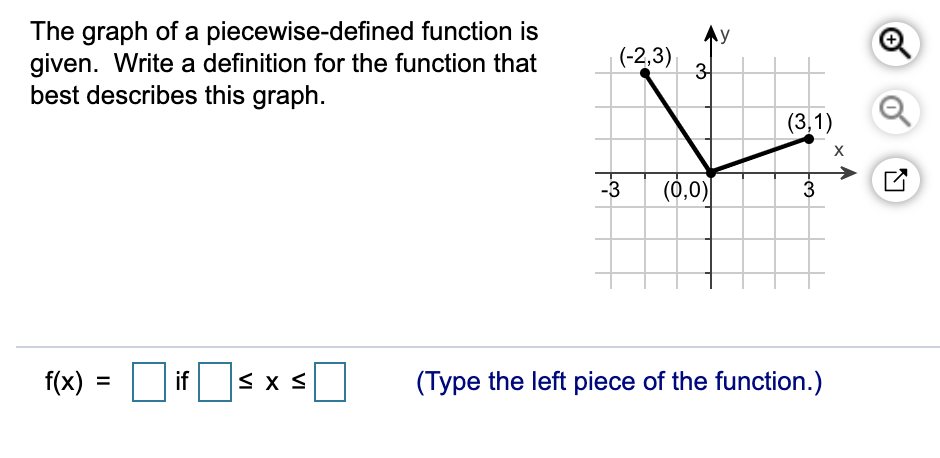
In the example above, the first piece only applies to “x” values that are greater than zero and less than three.
The domain restriction indicates which values of “x” this definition applies to. The function definition part is hopefully something you are thoroughly familiar with by now. Each line to the right of the curly brace contains two things: a function definition, and a “ domain restriction”. To the right of the curly brace are all the “pieces” of the function, as many as may be needed. To the right of the equal sign is a large curly brace, which serves as a vertical grouping symbol to contain the component parts of the piecewise function definition. Note that the definition begins exactly the way all function definitions do, with the name of the function (“f” in this case), followed by a set a parentheses that contains the list of inputs that the function requires (“x” in this case), and an equal sign. This can be modeled mathematically using a piecewise function: If a car gradually speeds up from zero to 30 miles per hour, then stays at that speed, the graph of this situation would look like this if each unit on the vertical axis represents 10 miles per hour, and the horizontal axis represents time: Both of these graphs are examples of “Piecewise Functions”, functions defined in a way that lets you mix and match as many separate components (pieces) as you wish. The graphs also show (in this case) two very different functions, but in a way that makes them look as though they are meant to represent a single, more complex function. Instead of being defined over all Real values of x, they start and stop at specific values. These graphs do not seem to follow all the rules you were taught for graphing lines or parabolas. And the green line stops at x = 5.5, just as it reaches the horizontal axis. And when x = 3 the blue parabola turns into a green line with a very different slope. It does not appear of the left of the vertical axis at all. In the graph on the right, note that the blue curve starts at x = 0. Furthermore, when x = 3 the blue line stops and the green line begins – but with a different slope. It does not appear to the left of the origin at all. In the graph on the left, note that the blue line starts at the origin. Two examples of such situations could be: The behavior being described might start at a specific time, or its nature changes at one or more points in time. While many relationships in our world can be described using a single mathematical function or relation, there are also many that require either more or less than what one equation describes.


 0 kommentar(er)
0 kommentar(er)
